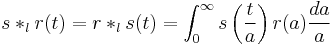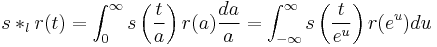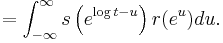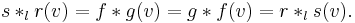Logarithmic convolution
The scale convolution of two functions 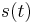 and
and 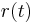 , also known as their logarithmic convolution is defined as the function
, also known as their logarithmic convolution is defined as the function
when this quantity exists.
Results
The logarithmic convolution can be related to the ordinary convolution by changing the variable from  to
to 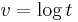 :
:
Define  and
and 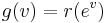 and let
and let 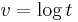 , then
, then
This article incorporates material from logarithmic convolution on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.